
A reader on Facebook asked me to write an article covering the nuances of Motion. As I thought about it, I wondered if there is a mathematical way to decide when a unit should attempt a Motion check. I researched the existing literature and found several articles covering AFV combat, but none specifically covering this topic so I set out to explore the idea.
The reality is this topic is situationally dependent. I think we can come up with some rules of thumb by the end of this article, but there will almost certainly be no hard and fast rules. In fact, to even study this problem I had to place a severe limitation on the situation: limit discussion to one tank versus another tank. I will discuss things beyond this scope later in the article, but there won’t be as much math associated with these latter topics.
Software
To accomplish this study, I wrote some Python code which modeled a contested Bounding First Fire shot, AKA Gun Duel. The bullets speak to the design of the code. It highlights what the code does, and just as importantly, does not do.
- The engagement lasts one shot for each side
- The second shooter has to survive to take a shot
- Each side rolls for depletable ammo
- Models APCR Penetration correctly
- Does not model AP Penetration correctly
- Correctly models Critical Hits
- Does not model Improbable Hits correctly
- Can determine turret/hull hits
- Bail outs because of Immobilization count as elimination
- Immobilization and Shock do not
- Each example was “replayed” 100K times to get the results.
Other Considerations
There are other things to consider when deciding to roll for Motion. As the Defender, if you survive, your Prep Fire is next. This means at least one shot, and possibly more if you get Rate Of Fire (ROF). Even if you lose ROF, the AFV in question can Intensive Fire (IF). Add to this, your Defensive First Fire shot places an Acquisition, which is doubled by your Prep Fire shot, and an Intensive Fire has a very good chance of hitting. When your chance of hitting is high, the limiting factor on “winning” will be the Final TK# used for the shot. This Prep Fire / IF consideration is outside the scope of the model but I do cover this situationally.
It is also worth noting that the B1F AFV could shoot in both B1F and AFPh. To do so, it must have maintained ROF in B1F AND not fire any other weapons during its MPh. I do not cover this aspect at all in this article.
In these examples, target size is not a factor. If applicable, target size can make the target easier or harder to shoot. What’s more, as B1F is generally a +4 DRM, adding a large target can change the original DR from a 6 to 7, a 16% increase in the base chance to hit. Said differently, that’s a 40% increased chance to hit moving from a Final 6 to Final 7. When dealing with Original DR in the range of 6 – 8, a single +1/-1 mod can make a significant difference. Don’t forget size modifiers!
These few considerations aren’t comprehensive. That isn’t possible. As you gain experience with ASL, you’ll get a feel for what matters and what doesn’t. Let’s look at some examples.
Example 1
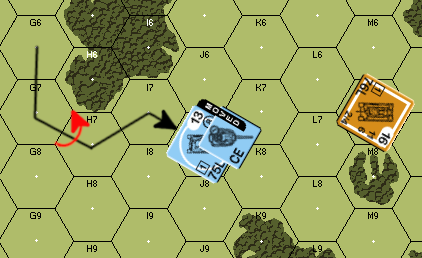
In this example, the PzIVH starts in G8. It moves to G7 and changes VCA/TCA. It then continues to move along the path highlighted by the arrow. Reaching J7, the PzIVH stops. The T34 M43 (hereafter just T34) declares a shot. The PzIVH declares a Gun Duel.
For this example, the PzIVH is the attacker, and the T34 is the defender. Understanding this is important to understanding the outcome below. For this engagement, the PzIVH is paying +2 Case B and +2 Case C firer-based DRM. The PzIVH has no target-based DRM. The T34 is paying +1 Case I firer-based DRM. It is also paying +2 Case J from the target-based DRM table. DRM and outcomes are shown in the table below. Since the T34 has the lower “firer-based” DRM, it will shoot first.
| T34 M43 | PzIVH | |
| Firer-based DRM | +1 | +4 |
| Target-based DRM | +2 | 0 |
| Win Percent | 20.85% | 12.36% |
| Hit% | 58.15% | 41.71% |
| Kill% (includes bailouts) | 20.85% | 15.61% |
| Shock% | 6.55% | 4.31% |
| Immobilization% | 3.36% | 3.07% |
| Bailout | .024% | .018% |
A Look At The Details
Because it has fewer Target-based DRM, the T34 ALWAYS shoots first. Under these circumstances, the T34 “wins” this engagement 20.85% of the time. I defined a “win” as “destroying the PzIVH or forcing the crew to bail out because of failing its Immobilization TC”. For the T34-who shot first-this is the same as its “kill” rate. Notice the PzIVH “killed” the T34 15.61% of the time but only “won” 12.36% of the time. The higher “kill rate” is because the PzIVH’s fewer chances were more “deadly”. Since the T34 wins the Gun Duel, it shoots EVERY time. The PzIVH must survive to shoot and it doesn’t do so ~21% of the time.
It is important to note; since the PzIVH does not win the Gun Duel, it shoots second. It does not survive 20.85% of the time. In the following PFPh, the T34 shoots first with a -1 Acq. The PzIVH will not be moving. This means the T34 will eliminate the PzIVH 25% of the time before the PzIVH can shoot back. If it gets to shoot back, the PzIVH will eliminate the T34 25.5% of the time. To avoid this, the T34 could opt for Intensive Fire (IF) with a -2 Acq offsetting the IF penalty. If it does IF, it eliminates the PzIVH 23.6% of the time, while Malfunctioning/Disabled 8.3% of the time. Together, the Prep Fire and IF shots eliminate the PzIVH 43% of the time. IMO, rolling for Motion in this circumstance is ill advised. The T34 should win this engagement more often than not.
Example 1B
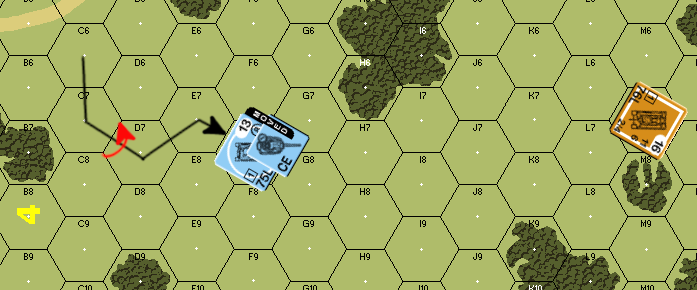
In this example, everything remains the same EXCEPT the range to target is now 7. For the T34, this means it is using a base TH# of 8. The PzIVH is using a base of 9. All other DRM remain unchanged. How does this affect the outcome?
| T34 M43 | PzIVH | |
| Firer-based DRM | +1 | +4 |
| Target-based DRM | +2 | 0 |
| Win Percent | 10.68% | 9.85% |
| Hit% | 27.58% | 27.73% |
| Kill% (includes bailouts) | 10.68% | 11.03% |
| Shock% | 2.96% | 2.9% |
| Immobilization% | 1.48% | 1.9% |
| Bailout | .011% | .012% |
A Look At The Details
Again, the T34 shoots first. (Can you see why?) The T34 “wins” this engagement just 10.68% of the time. Compare that to the PzIVH’s win rate of 9.85%. Even though the T34 gets the next shot in its PFPh, it only has a 20.4% chance to kill the PzIVH compared to the PzIVH’s 23.2% chance to kill it. If it opts for IF, the T34 eliminates the PzIVH 17.3% of the time with an 8.3% chance for Malfunction/Disable of the MA. Together, the Prep Fire and IF shots eliminate the PzIVH 34.2% of the time.
This situation slightly favors the T34 and most of that favor is because of its opportunity to fire and IF first. The T34 is “favored” to win this engagement in the next turn by ~14% but at an 8% risk of Malfunctioning/Disabling the MA. Motion here might be slightly favorable to avoid the chance for Malfunction/Disable but opting to fight it out is not a terrible decision either. The VC would drive my decision, but absent any other considerations, I would opt for Motion and be OK with slugging it out in this case.
Example 2
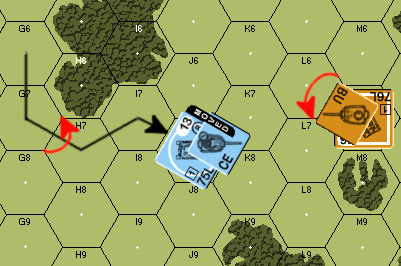
Ostensibly, this setup is the same as example 1. The difference is the T34 begins with its TCA pointing at the M7/L6/M6 vertex. It must change the TCA to engage the PzIVH when it gets to J7. This TCA change adds a +2 Case A DRM to the T34’s shot. In addition, the PzIVH is facing the T34’s Hull Side Armor. As a hull is the likeliest outcome, it will be easier to kill the T34. All other DRM remain unchanged. How does this affect the outcome?
| T34 M43 | PzIVH | |
| Firer-based DRM | +3 | +4 |
| Target-based DRM | +2 | 0 |
| Win Percent | 10.7% | 14.1% |
| Hit% | 27.58% | 41.82% |
| Kill% (includes bailouts) | 10.7% | 15.79% |
| Shock% | 2.94% | 4.34% |
| Immobilization% | 1.48% | 3.11% |
| Bailout | .011% | .012% |
A Look At The Details
Again, the T34 shoots first and “wins” this engagement 10.7% of the time while the PzIVH shoots second and “wins” this engagement 14.1% of the time. Changing TCA increases the PzIVH’s survivability by ~10% compared to the earlier example. The increased survivability and weaker hull side armor is enough to “win” the engagement for the PzIVH by ~3.5%. Shock and Immobilization percentages tip the B1F engagement further into the PzIVH’s favor.
The T34 shoots next in PFPh. These odds remain unchanged from those in example 1. The PzIVH has the T34’s hull side so its odds are much better this time. The PzIVH kills the T34 59.2% of the time if it survives Prep Fire. Even if it opts to Prep Fire and Intensive Fire, the T34 is less likely to kill the PzIVH than it is to be killed by the PzIVH (42.7% in favor of the T34 versus 59.2% for the PzIVH). This overall engagement favors the PzIVH, significantly so if the T34 decides against IF. In this situation, I think this is a clear cut call to roll for Motion, especially if there is a clear opportunity for a Motion Escape. But again, this will be dependent on outside factors.
Example 2B

This is ostensibly the same engagement as example 2 except the range to target is now 7 hexes. All DRM remain the same. Let’s see how this changes the engagement.
| T34 M43 | PzIV H | |
| Firer-based DRM | +3 | +4 |
| Target-based DRM | +2 | 0 |
| Win Percent | 4.53% | 10.54% |
| Hit% | 8.35% | 27.82% |
| Kill% (includes bailouts) | 4.53% | 11.03% |
| Shock% | .074% | 2.88% |
| Immobilization% | .029% | 1.9% |
| Bailout | .002% | .013% |
A Look At The Details
The PzIVH shoots second and “wins” 10.54% of the time while the T34 shoots first and “wins” 4.53% of the time. This is a nearly 2:1 ratio in favor of the PzIVH even though it must survive the first shot to have a chance. For the T34, this is far from ideal.
If the T34 survives, it shoots next in its upcoming PFPh. The T34’s chances remain unchanged from example 1B. The PzIVH’s chances have changed significantly because of attacking the T34’s hull side. Now, the PzIVH eliminates the T34 51.5% of the time. Even if the T34 opts to IF in PFPh, the combined odds amount to a 34.2% chance to eliminate the PzIVH. This engagement clearly favors the PzIVH, even more so if the T34 isn’t willing to IF. In all but the most dire of situations, I would roll for Motion.
Example 3
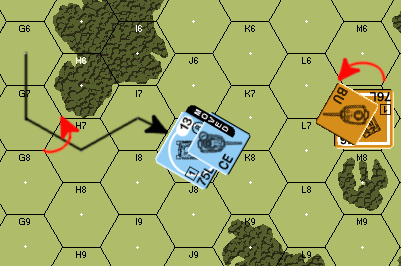
This example is mostly the same as Example 2. The T34 changes the VCA instead of the TCA. The Case A DRM is now +3. All other DRM remain the same.
The engagement has changed significantly though. With the +3 Case A DRM, firer-based DRM are now the same (+4 B/C for the PzIVH, +3 A, +1 I for the T34) so the “roll off” applies to this engagement to see who shoots first (C2.2401). While the firer-based DRM are equal, the T34 has to also pay for Case J. The first shooter is determined by adding a DR to all applicable DRM and see which total is less than the other. If they tie, the shots occur simultaneously. Because the T34 is paying an additional +2 for Case J, it will shoot second more often than it does first. Let’s see how this affects the engagement.
| T34 M43 | PzIVH | |
| Firer-based DRM | +4 | +4 |
| Target-based DRM | +2 | 0 |
| Win Percent | 6.54% | 15.35% |
| Hit% | 17.73% | 42.57% |
| Kill% (includes bailouts) | 7.62% | 16.12% |
| Shock% | 1.59% | 4.38% |
| Immobilization% | 1.04% | 3.19% |
| Bailout | .006% | .022% |
| Mutual Destruction | .003% | .003% |
A Look At The Details
The PzIVH “wins” the engagement 15.35% of the time. The T34 “wins” the engagement 6.54% of the time. Remember though, the software does not model Improbable Hits correctly. If the software identifies an Improbable Hit, all such hits are modeled as Critical Hits. As such, the T34s “win rate” is inflated here. Even so, this is a greater than 2:1 advantage in favor of the PzIVH. The Mutual Destruction shows how often both sides eliminate each other on a tie (C2.2401).
All the odds for the next PFPh remain the same as calculated in example 2. Given that, this example is even more so in favor of attempting Motion. The PzIVH’s chances have increased in B1F while the T34’s have decreased. Given that and the previously discussed PFPh odds, this example is even more so in favor of attempting Motion.
Example 3B – T34 Opts for Motion
Refer to example three. Assume rather than shooting, the T34 successfully makes a Motion roll and changes TCA/VCA as part of the Motion Roll, exposing turret front and hull side armor.
| T34 M43 | PzIVH | |
| Firer-based DRM | +5 | +4 |
| Target-based DRM | +2 | +2 |
| Win Percent | 4.23% | 7.38% |
| Hit% | 8.37% | 16.58% |
| Kill% (includes bailouts) | 4.56% | 7.38% |
| Shock% | .73% | 1.42% |
| Immobilization% | .31% | 1.09% |
| Bailout | .002% | .008% |
A Look At The Details
In this situation, the PzIVH shoots first and “wins” just 7.38% of the time, a ~8% increase in survivability. For this increased survivability, the T34 sacrifices shooting first, “winning” the engagement only 4.23% of the time. Again, keep in mind this rate is inflated due to software limitations. The sacrifices for the T34 do not stop there.
The T34 surrenders the next shot to the PzIVH in the upcoming DFPh. If the T34 cannot execute a Motion Escape, the PzIVH eliminates it 51.5% of the time. The T24 could opt to stop and shoot but the PzIVH wins the Gun Duel and achieves the same kill rate. The T34 is probably best served taking its lumps and going down swinging.
Example 4
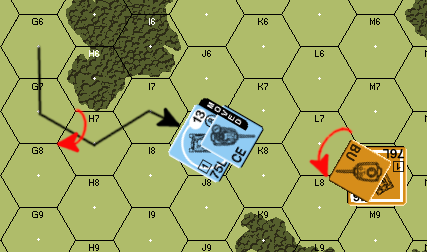
This example is the same as example 2 except this time, the T34 is in a woods Location. This doubles the TCA TH DRM to +4. It gains a +1 target-based DRM for the TEM.
This is a VERY significant change. Until now, the T34 has either won the Gun Duel and shot first, or rolled off to see who shoots first. The T34 loses the Gun Duel here. Accordingly, the PzIVH will shoot first. Let’s see what this looks like.
| T34 M43 | PzIVH | |
| Firer-based DRM | +5 | +4 |
| Target-based DRM | +2 | 0 |
| Win Percent | 2.82% | 15.72% |
| Hit% | 8.73% | 41.42% |
| Kill% (includes bailouts) | 4.53% | 15.72% |
| Shock% | .72% | 4.24% |
| Immobilization% | .34% | 3.05% |
| Bailout | .002% | .022% |
A Look At The Details
The PzIVH “wins” this engagement 15.72% of the time. The T34 “wins” a mere 2.82% of the time. This is more than a 5:1 ratio in favor of the PzIVH. If it survives, the T34 shoots next in its upcoming PFPh. The outcome of that PFPh analysis is the same as example 2.
This time, taking Motion is not likely to help here. Changing VCA to get away will cause at least one Bog check. In addition, if the T34 opts for Motion, the Attacker has little to fear from the T34 since there is ~3% chance of elimination. It could delay its shot until AFPh and gain an acquisition making its TH chance even better in its upcoming DFPh. This is a bad engagement for the T34, a situation it should seek to avoid. While its odds of survival are not great, going down swinging is a better option than Motion here. Perhaps the dice will bail you out.
Of course, there is also Reverse Motion. Declaring Reverse Motion and backing out into N8 could save the T34. Surprisingly, knowing the rules can generate more options for survival.
Example 4B – Attacker Closes To Point Blank Range
Refer to example 4. This time, the PzIVH stops in K8. All DRM remain the same except each side now gets a -1 Case L target-based DRM. If they get special ammo, the TK# goes up by 1. Even with the change in DRM, the PzIVH will always shoot first.
| T34 M43 | PzIVH | |
| Firer-based DRM | +4 | +3 |
| Target-based DRM | +1 | -1 |
| Win Percent | 5.54% | 21.14% |
| Hit% | 16.71% | 57.99% |
| Kill% (includes bailouts) | 7.03% | 21.14% |
| Shock% | 1.48% | 6.46% |
| Immobilization% | .95% | 4.11% |
| Bailout | .005% | .03% |
A Look At The Details
In this situation, the PzIVH shoots first and “wins” 21.14% of the time. The T34 only “wins” 5.54% of the time. Each side gets more deadly and the “win” ratio falls to 4:1 in favor of the PzIVH. Still, the T34 doesn’t even get to shoot back 21.14% of the time. Albeit slim, the 6% increase for the PzIVH just makes a bad situation worse for the T34.
Assume the PzIVH closes to L8. Now the Case L DRM increases to -2. The PzIVH shoots first and “wins” 25.81% of the time while the T34 “wins” 7.96% of the time. The kill ratio comes down to ~3:1 in favor of the PzIVH as the engagement becomes even more deadly. Now the T34 doesn’t even get to shoot back 1 in 4 times.
In each case, rolling for Motion makes little sense [EXC: Reverse Motion]. There is a significant chance of losing the T34 for nothing gained. Rolling a TH DR might just bail you out of this situation but don’t count on it. Better yet, hope you recognize how lucky you were so you don’t learn the wrong lesson. Sadly, wrong lessons can be VERY hard to identify and remove from your game play.
What Else Affects The Decision

It is nearly impossible to list all the reasons to roll for, or not roll for, Motion. As I have said in other articles, your decision making should be driven by the Victory Conditions (VC). What follows is merely food for thought. I do not intend it to be comprehensive:
- If the VC requires a surviving AFV, it might be more prudent to stay and fight against the last AFV than it is to roll for Motion.
- Alternatively, if your defending AFV is the last one, rolling for Motion might make the most sense.
- I have stated elsewhere, an unsupported AFV in Motion is already dead. If there are more enemy AFV around, they could swarm and eliminate the Motion AFV with nothing to show for the loss. In these situations, it is probably better to go down swinging.
- If the possibility of a Motion Escape exists, living to fight another day is rarely a bad decision. The AFV may still die with nothing to show for it, so weigh this decision carefully.
- If you make a Motion roll, don’t forget to try for any Smoke Dispenser you may have. The Smoke will disappear in your next Prep Fire Phase but it will help the AFV survive to the MPh. When combined with a Motion Escape this can be powerful.
- Don’t forget an AFV can freely change VCA/TCA as part of a Motion dr. It can make a free VCA/TCA change in Defensive Fire. You can use the first to point the thickest armor at the Attacker and the second to plan your escape in the next Mph. If you haven’t already, I recommend you read my The Basics of AFV Combat In ASL: Tank vs. Tank. That article goes into much deeper detail on the Dance of Death.
Incorporating This Into Your Game Play

You need to recognize players are going to hunt your tanks down and try to eliminate them. From this article, I hope it has become apparent how important planning your escape as part of the AFV’s movement is. If you don’t have an escape, you need to have some sort of covering AT fire. An isolated AFV is a dead AFV just waiting to learn its fate.
The first question of Motion is “Can I get away?”. If the answer to this question is “no”, is there a supporting unit covering the AFV with fire? If not, you should be prepared to take your lumps. You either deliberately parked the AFV there for a reason (remember, plan ahead right) or didn’t think about it and now you are being punished for lack of planning. In either case, a successful Motion attempt runs a significant risk of losing this AFV for nothing.
If you can get away, a second question is “Can other AFVs come to bear making the escape unlikely?”. Do you have a unit offering covering fire against this new incursion? If not, again you’re going to have to take your lumps. A burnt hand is the best teacher. You just need to remember the burn and learn the lesson.
Conclusion
From this look, we can draw a couple of conclusions. Sadly, none of these conclusions will be hard and fast rules. Like all things in ASL, the answer will be situationally dependent.
When the Attacker has the firer-based DRM advantage, rolling for Motion becomes a more reasonable option for the defender. This becomes a much easier call if the AFV can make a Motion Escape. Even if the Motion Escape is available, it is possible to lose the Defending AFV for nothing.
DRM translates into survivability. As the Attacker, you want the Defender to have as many of these as you can. Not only does this increase your odds of survival, as they approach parity and beyond, your chance to shoot first increases. This makes it possible to eliminate the Defender before it even gets to shoot back.
Finally, special ammo makes close range combat even more deadly. This should not come as a surprise to anyone. But this deadly close range combat can be VERY punishing to a side which shoots second as they may not survive to shoot back. This can make a decision to attempt a Motion dr easier, but you must still consider everything else I have talked out here–and more. Like most things in ASL, a Motion dr is a two-edged sword. I hope this helps! – jim
Acknowledgements
I would be remiss to not mention Bruce Bakken’s Panzer Gegen Panzer in the 93a ASL Anual. It was one of the earliest articles covering this topic. Ole Boe’s Stop And Go Traffic in the 96 ASL Anual is another early work on the topic. While still relevant today, some rules have changed since these articles were written. Take caution when seeing something that makes little sense. The rule may have changed. Still, both articles remain excellent resources for learning good play.
Matt Shostak wrote a series of articles for Banzai Pipeline which used a similar technique to what I did here. While Matt and I arrived at our method independently, his work precedes mine and deserves recognition for his pioneering effort. Matt’s earlier work is in Banza! issues 12-2, 12-3, 13-1, and 16-2. These issues are available via the Banzi!! Index.
I also received some valuable input from fellow ASL’ers. Mike Balis, Geoff Wessendorf, and the ever shy Hong Kong Wargamer helped me to refine and focus the article. Geoff suggested the tables which really helped a lot. J.R. VanMechelen helped me with the math. He has not checked all of the outcome so those mistakes remain my own. I just needed a sanity check and he helped provide it. Thanks guys. I really appreciate all your help and input. You made this better.

